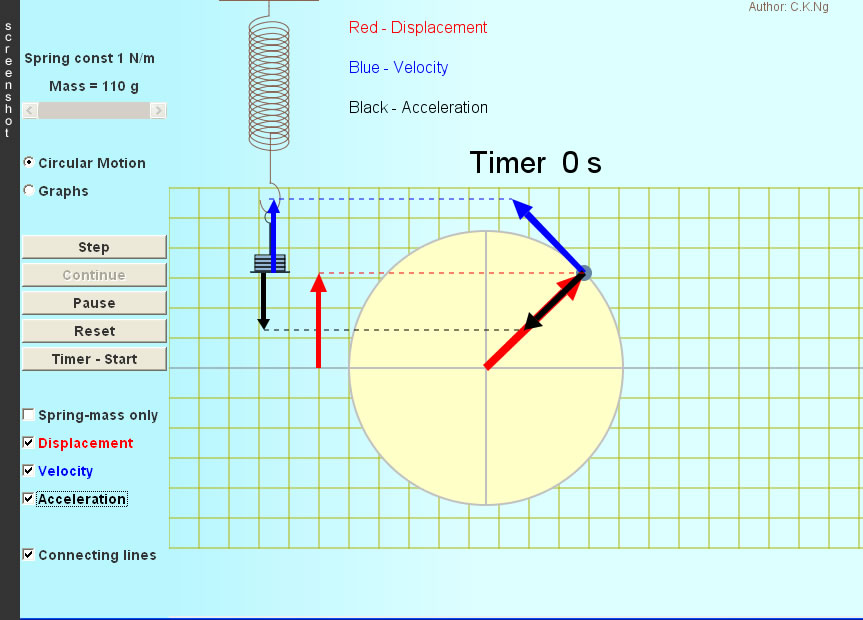
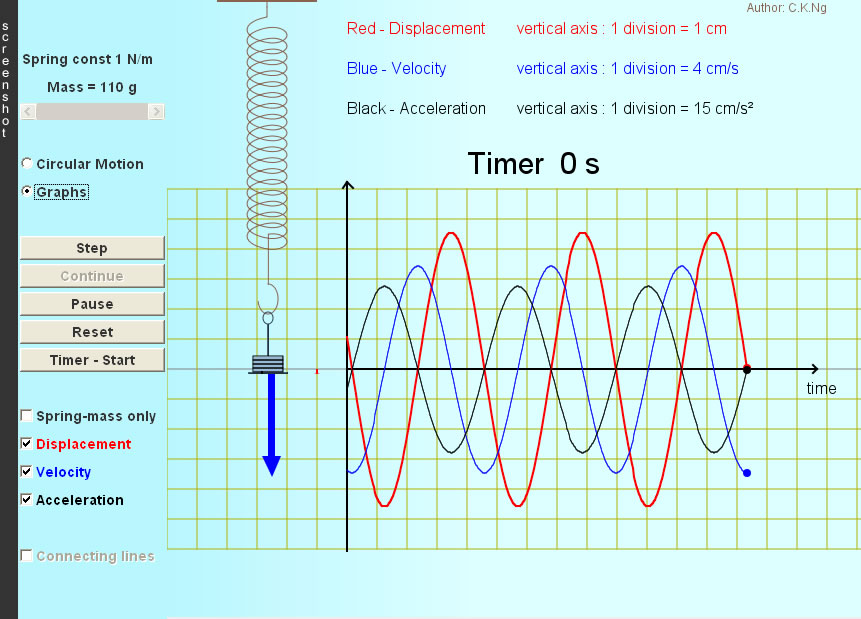
Spring-Mass SHM (Kinematics)
To begin an oscillation, drag the block up or down and then release.
The periodic motion of the block is simple harmonic because the acceleration is always proportional, but opposite to the displacement from the equilibrium position (definition of SHM).
Properties of SHM:
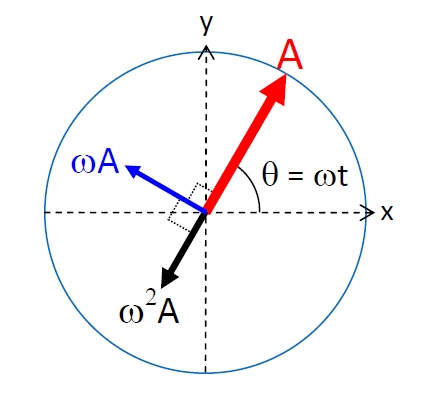
- It is identical to the projection of a uniform circular motion on an axis.
- The curves (x-t, v-t and a-t) are sinusoidal with acceleration leading velocity by π/2 and velocity leading displacement by π/2.
- The period of oscillation is independent of amplitude (isochronism).
|
Internal Links : |
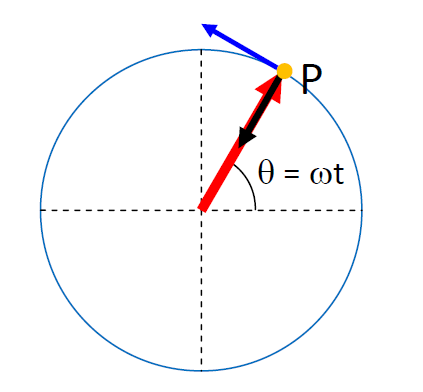
|
|
|
|