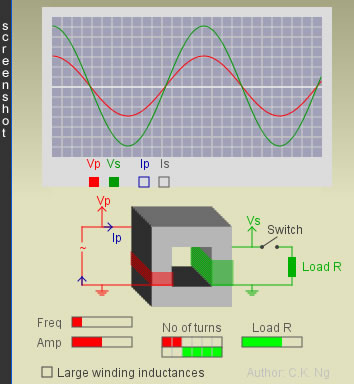
Define

Suppose the following conditions are satisfied:

1. The two coils are resistanceless.
   Voltage across the primary coil, .....(1)
   Voltage across the secondary coil, .....(2)
   
   
2. There is no flux leakage, i.e., Φ _p = Φ _s .....(3)

From (1), (2) and (3), we get

Remarks

1. Secondary coil is on open circuit

   1. The primary coil behaves as a pure inductor.
   2. The only current flowing is the primary current (I_p).
   3. The flux linking the two coils is caused by I_p. This primary current is called magnetizing current (I_p,M).
   4. The primary voltage (V_p) leads the magnetizing current (I_p,M) by π/2.
   5. Average input power = 0

2. Resistive load R is connected to the secondary coil

   1. The secondary current (I_s) becomes nonzero.
   2. I_s is always in phase with V_s, because the load is a pure resistor.
   3. The flux linking the two coils is still caused by I_p,M.
   4. Besides the manetizing current, the primary current has one more component (call it I_p,L), which is anti-phase with the secondary current I_s, i.e., I_p = I_p,M + I_p,L, where I_p,M and I_p,L are π/2 out of phase.

      By Lenz’s law, I_s must flow in a direction such that the change of magnetic flux in the core is reduced. However, the change of flux in the core always produces a voltage in the primary coil to have the same value as the a.c. source voltage (since the input loop is resistanceless). To maintain this, the primary current eventually becomes larger to restore the original magnetic flux, compensating the opposition due to the secondary current. Eventually, the core flux is still produced by I_p,M,while the fluxes produced by I_p,L and I_s cancel each other out.

   5. The primary voltage (V_p) leads the primary current (I_p) by an angle θ = tan^-1( R/X_s), where X_s is the reactance of the secondary coil.
   6. Average input power = V_p,rmsI_p,rmscos(θ)

3. If the load R is decreased,

   1. I_p,L will be further increased, but I_p,M remains the same, and
   2. the phase angle between the primary voltage and the primary current will be further reduced, approaching zero.

4. When the load R << X_s (reactance of the secondary coil),

   1. I_p,L >> I_p,M, hence I_p ≈ I_p,L, and
   2. the primary voltage is (nearly) in-phase with the primary current.
      Any time, V_pI_p,L = V_sI_s
      Now,V_pI_p = V_sI_s
      Therefore, I_p : I_s = V_s : V_p = N_s : N_p

5. It is noteworthy that

   1. the voltage ratio V_s : V_p = N_s : N_p holds under the two assumptions (i) coils are resistanceless, and (ii) no flux leakage. No matter the secondary coil is open or not, the resistance of R is large or small, the voltage ratio holds, and
      
   2. the current ratio I_p : I_s = N_s : N_p holds when, besides the transformer satisfying the above two assumptions, the resistance of the load R must be sufficiently small (R << X_s).