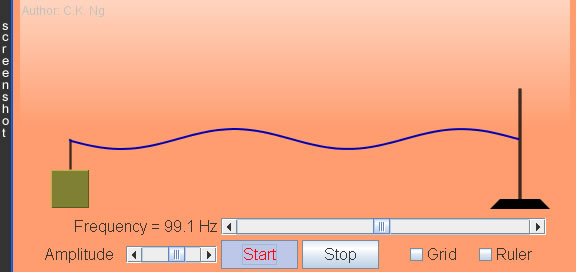
Generating Standing Waves in String (Resonance)
The length of the string can be varied by dragging the stand to the left/right.
The tension in the string can hence be changed.
|
Internal Links : |
- A stationary wave is produced when the wavelength of the wave in the string being fixed at its two ends satisfies λn = 2L/n, where L is the length of the string and n = 1, 2, 3,…
- When a stationary wave of wavelength λn is formed, there are n
loops
formed in the string.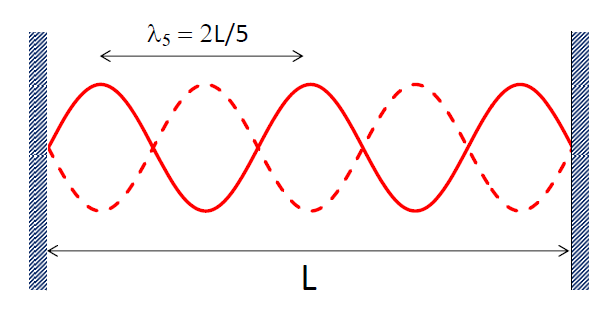
- Each stationary wave is a normal mode of the system.
- Besides the normal modes, the string has infinite modes of oscillations, e.g., plucking the string at any point on it. However, any mode can be represented by a series sum of the normal modes of different amplitudes. An analogy in mathematics is that any 3D vector can be expressed like P→ = a i→ + b j→+ c k→, where i→, j→ and k→ are the unit vectors.
- The system is forced to oscillate when a periodic force is applied to it. When the frequency of the periodic force matches with one of the frequencies fn = wave speed / λn, resonance will occur. Then, stationary wave of that normal mode appears on the string.
- When the system is forced to oscillate at off-resonance, the oscillation is a combination of the neighboring modes. The resultant amplitude is usually small becuse none of the normal modes is dominant.